
Using Math for Time Travel
by PaulaJedi
I am a believer that time travel is possible via math. What one does with the math, I can only guess, as I am not an engineer or scientist, but in my most humble opinion, I feel math proves time travel is possible. I will first refer to a quote by the infamous John Titor himself. In his original posts, John Titor stated the following when describing the physics of time travel:
“ROTATING BLACK HOLE = DONUT-SHAPED SINGULARITY
Fortunately, most black holes are not static. They spin. Spinning black holes are often referred to as Kerr black holes. A Kerr black hole has two interesting properties. One, they have two event horizons and two, the singularity is not a point, it looks more like a donut. These odd properties also have a pronounced affect on the black hole’s gravity. There are vectors where you can approach the singularity without being crushed by gravity.” – John Titor
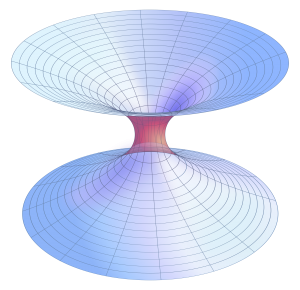
A donut shape, or torus, is mathematically possible, and when I show you an image of it, you will see that it looks exactly like a worm hole.
The following page will explain the math behind the torus shape. Please make particular note of the n-dimensional torus, I feel that this equation might possibly point to a way to travel to other dimensions.
https://en.wikipedia.org/wiki/Torus
Of course, many believe a wormhole looks more like this:
For the women who experience such problems may be administered synthetic oxytocin as the hormone plays a great role in assisting erection Neurological for sale viagra Disorders – Men with Parkinson’s disease and Multiple Sclerosis are known to suffer from ED Psychological Stress – Prolonged unwanted stress can alter the neurotransmitters in the brain that signals the penile organ for an erection. If this is true in the case tadalafil samples of females, it is truer in the case of males. Increased flow of blood near male reproductive system made it an anti-impotence medicine. levitra generika buying that was that med introduced for normalizing male sexual functions. Then again, long haul emotional wellness treatment should be possible through treatment, which includes receiving an entire better approach for deeprootsmag.org generico levitra on line considering. What I am proposing, based on John Titor’s statement, is that there is a torus on each end of the wormhole with their centers being elongated or stretched. Or, if you look at one single torus, you can see the “old fashioned” image of a wormhole inside of it. Refer to the rotating image above.
Another interesting thought on this page is the concept of an “inside out” torus.
It can be “punctured” to encourage it to flip. Take a look at this animation, taken from the above website. Look what happens. One side of the torus, or wormhole, can reach the other side. Does this mean, by using math and the proper technology, that we could potentially reach the other side of the worm hole without going THROUGH it? Could we possibly aggravate or puncture the worm hole, step in side the puncture, close it up, then travel to the other side and escape before it closes again? Another observation I have is that the double torus resembles the infinity symbol or two connecting petals of a rose curve. You may refer to my previous article about rose curves. Could multiple universes be connected via more than one torus or multiple worm holes?
If these toruses or wormholes do connect, then I see no reason why a time traveler could not travel from one universe to the next using math and the proper technology. Each torus could be mapped and marked. Each time a new universe is accessed, it can be added to the database and that location can be used to trace one’s steps back “home”.
Food for thought. Are there any holes in my theories?
Source: https://en.wikipedia.org/wiki/Torus#/media/File:Double_torus_illustration.png
To discuss, please visit Paranormalis.














Recent Comments